Code
import numpy as np
import matplotlib.pyplot as plt
from lab_utils_multi import zscore_normalize_features, run_gradient_descent_feng
np.set_printoptions(precision=2) # reduced display precision on numpy arrayskakamana
April 24, 2023
you’ll see some code that implements polynomial regression including features like x, x squared, and x cubed.
This Feature engineering and polynomial regression is part of DeepLearning.AI course: Machine Learning Specialization / Course 1: Supervised Machine Learning: Regression and Classification In this course we will learn the difference between supervised and unsupervised learning and regression and classification tasks. Develop a linear regression model. Understand and implement the purpose of a cost function. Understand and implement gradient descent as a machine learning training method.
This is my learning experience of data science through DeepLearning.AI. These repository contributions are part of my learning journey through my graduate program masters of applied data sciences (MADS) at University Of Michigan, DeepLearning.AI, Coursera & DataCamp. You can find my similar articles & more stories at my medium & LinkedIn profile. I am available at kaggle & github blogs & github repos. Thank you for your motivation, support & valuable feedback.
These include projects, coursework & notebook which I learned through my data science journey. They are created for reproducible & future reference purpose only. All source code, slides or screenshot are intellectual property of respective content authors. If you find these contents beneficial, kindly consider learning subscription from DeepLearning.AI Subscription, Coursera, DataCamp
In this lab you will: - explore feature engineering and polynomial regression which allows you to use the machinery of linear regression to fit very complicated, even very non-linear functions.
You will utilize the function developed in previous labs as well as matplotlib and NumPy.
# Feature Engineering and Polynomial Regression Overview
Out of the box, linear regression provides a means of building models of the form: \[f_{\mathbf{w},b} = w_0x_0 + w_1x_1+ ... + w_{n-1}x_{n-1} + b \tag{1}\] What if your features/data are non-linear or are combinations of features? For example, Housing prices do not tend to be linear with living area but penalize very small or very large houses resulting in the curves shown in the graphic above. How can we use the machinery of linear regression to fit this curve? Recall, the ‘machinery’ we have is the ability to modify the parameters \(\mathbf{w}\), \(\mathbf{b}\) in (1) to ‘fit’ the equation to the training data. However, no amount of adjusting of \(\mathbf{w}\),\(\mathbf{b}\) in (1) will achieve a fit to a non-linear curve.
Above we were considering a scenario where the data was non-linear. Let’s try using what we know so far to fit a non-linear curve. We’ll start with a simple quadratic: \(y = 1+x^2\)
You’re familiar with all the routines we’re using. They are available in the lab_utils.py file for review. We’ll use np.c_[..] which is a NumPy routine to concatenate along the column boundary.
# create target data
x = np.arange(0, 20, 1)
y = 1 + x**2
X = x.reshape(-1, 1)
model_w,model_b = run_gradient_descent_feng(X,y,iterations=1000, alpha = 1e-2)
plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("no feature engineering")
plt.plot(x,X@model_w + model_b, label="Predicted Value"); plt.xlabel("X"); plt.ylabel("y"); plt.legend(); plt.show()Iteration 0, Cost: 1.65756e+03
Iteration 100, Cost: 6.94549e+02
Iteration 200, Cost: 5.88475e+02
Iteration 300, Cost: 5.26414e+02
Iteration 400, Cost: 4.90103e+02
Iteration 500, Cost: 4.68858e+02
Iteration 600, Cost: 4.56428e+02
Iteration 700, Cost: 4.49155e+02
Iteration 800, Cost: 4.44900e+02
Iteration 900, Cost: 4.42411e+02
w,b found by gradient descent: w: [18.7], b: -52.0834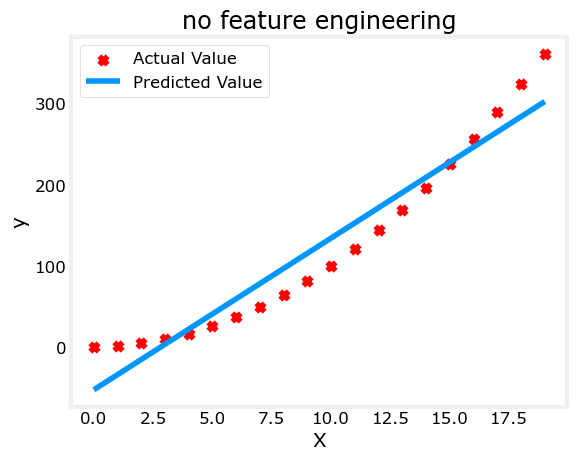
Well, as expected, not a great fit. What is needed is something like \(y= w_0x_0^2 + b\), or a polynomial feature. To accomplish this, you can modify the input data to engineer the needed features. If you swap the original data with a version that squares the \(x\) value, then you can achieve \(y= w_0x_0^2 + b\). Let’s try it. Swap X for X**2 below:
X = X.reshape(-1, 1) #X should be a 2-D Matrix
model_w,model_b = run_gradient_descent_feng(X, y, iterations=10000, alpha = 1e-5)
plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Added x**2 feature")
plt.plot(x, np.dot(X,model_w) + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()Iteration 0, Cost: 7.32922e+03
Iteration 1000, Cost: 2.24844e-01
Iteration 2000, Cost: 2.22795e-01
Iteration 3000, Cost: 2.20764e-01
Iteration 4000, Cost: 2.18752e-01
Iteration 5000, Cost: 2.16758e-01
Iteration 6000, Cost: 2.14782e-01
Iteration 7000, Cost: 2.12824e-01
Iteration 8000, Cost: 2.10884e-01
Iteration 9000, Cost: 2.08962e-01
w,b found by gradient descent: w: [1.], b: 0.0490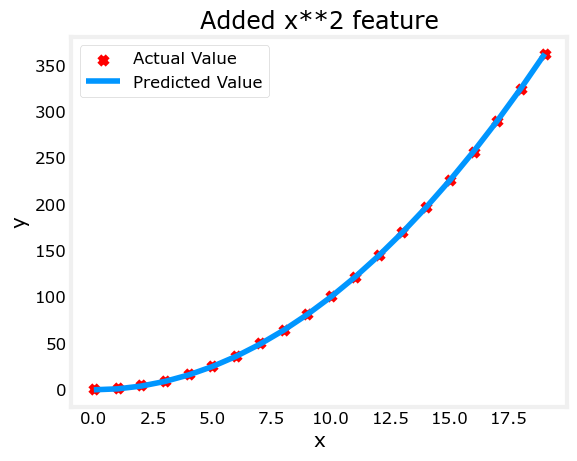
Great! near perfect fit. Notice the values of \(\mathbf{w}\) and b printed right above the graph: w,b found by gradient descent: w: [1.], b: 0.0490. Gradient descent modified our initial values of $,b $ to be (1.0,0.049) or a model of \(y=1*x_0^2+0.049\), very close to our target of \(y=1*x_0^2+1\). If you ran it longer, it could be a better match.
Above, we knew that an \(x^2\) term was required. It may not always be obvious which features are required. One could add a variety of potential features to try and find the most useful. For example, what if we had instead tried : \(y=w_0x_0 + w_1x_1^2 + w_2x_2^3+b\) ?
Run the next cells.
Iteration 0, Cost: 1.14029e+03
Iteration 1000, Cost: 3.28539e+02
Iteration 2000, Cost: 2.80443e+02
Iteration 3000, Cost: 2.39389e+02
Iteration 4000, Cost: 2.04344e+02
Iteration 5000, Cost: 1.74430e+02
Iteration 6000, Cost: 1.48896e+02
Iteration 7000, Cost: 1.27100e+02
Iteration 8000, Cost: 1.08495e+02
Iteration 9000, Cost: 9.26132e+01
w,b found by gradient descent: w: [0.08 0.54 0.03], b: 0.0106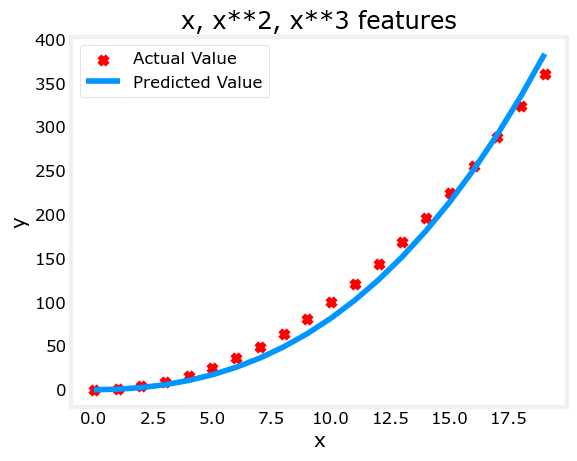
Note the value of \(\mathbf{w}\), [0.08 0.54 0.03] and b is 0.0106.This implies the model after fitting/training is: \[ 0.08x + 0.54x^2 + 0.03x^3 + 0.0106 \] Gradient descent has emphasized the data that is the best fit to the \(x^2\) data by increasing the \(w_1\) term relative to the others. If you were to run for a very long time, it would continue to reduce the impact of the other terms. >Gradient descent is picking the ‘correct’ features for us by emphasizing its associated parameter
Let’s review this idea: - Intially, the features were re-scaled so they are comparable to each other - less weight value implies less important/correct feature, and in extreme, when the weight becomes zero or very close to zero, the associated feature is not useful in fitting the model to the data. - above, after fitting, the weight associated with the \(x^2\) feature is much larger than the weights for \(x\) or \(x^3\) as it is the most useful in fitting the data.
Above, polynomial features were chosen based on how well they matched the target data. Another way to think about this is to note that we are still using linear regression once we have created new features. Given that, the best features will be linear relative to the target. This is best understood with an example.
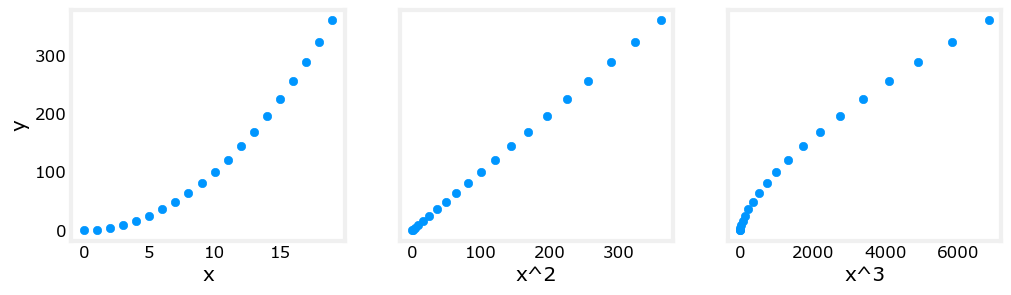
Above, it is clear that the \(x^2\) feature mapped against the target value \(y\) is linear. Linear regression can then easily generate a model using that feature.
As described in the last lab, if the data set has features with significantly different scales, one should apply feature scaling to speed gradient descent. In the example above, there is \(x\), \(x^2\) and \(x^3\) which will naturally have very different scales. Let’s apply Z-score normalization to our example.
Peak to Peak range by column in Raw X:[ 19 361 6859]
Peak to Peak range by column in Normalized X:[3.3 3.18 3.28]Now we can try again with a more aggressive value of alpha:
x = np.arange(0,20,1) y = x**2
X = np.c_[x, x2, x3] X = zscore_normalize_features(X)
model_w, model_b = run_gradient_descent_feng(X, y, iterations=100000, alpha=1e-1)
plt.scatter(x, y, marker=‘x’, c=‘r’, label=“Actual Value”); plt.title(“Normalized x x2, x3 feature”) plt.plot(x,X@model_w + model_b, label=“Predicted Value”); plt.xlabel(“x”); plt.ylabel(“y”); plt.legend(); plt.show()
Feature scaling allows this to converge much faster. Note again the values of \(\mathbf{w}\). The \(w_1\) term, which is the \(x^2\) term is the most emphasized. Gradient descent has all but eliminated the \(x^3\) term.
With feature engineering, even quite complex functions can be modeled:
x = np.arange(0,20,1)
y = np.cos(x/2)
X = np.c_[x, x**2, x**3,x**4, x**5, x**6, x**7, x**8, x**9, x**10, x**11, x**12, x**13]
X = zscore_normalize_features(X)
model_w,model_b = run_gradient_descent_feng(X, y, iterations=1000000, alpha = 1e-1)
plt.scatter(x, y, marker='x', c='r', label="Actual Value"); plt.title("Normalized x x**2, x**3 feature")
plt.plot(x,X@model_w + model_b, label="Predicted Value"); plt.xlabel("x"); plt.ylabel("y"); plt.legend(); plt.show()Iteration 0, Cost: 2.20188e-01
Iteration 100000, Cost: 1.70074e-02
Iteration 200000, Cost: 1.27603e-02
Iteration 300000, Cost: 9.73032e-03
Iteration 400000, Cost: 7.56440e-03
Iteration 500000, Cost: 6.01412e-03
Iteration 600000, Cost: 4.90251e-03
Iteration 700000, Cost: 4.10351e-03
Iteration 800000, Cost: 3.52730e-03
Iteration 900000, Cost: 3.10989e-03
w,b found by gradient descent: w: [ -1.34 -10. 24.78 5.96 -12.49 -16.26 -9.51 0.59 8.7 11.94
9.27 0.79 -12.82], b: -0.0073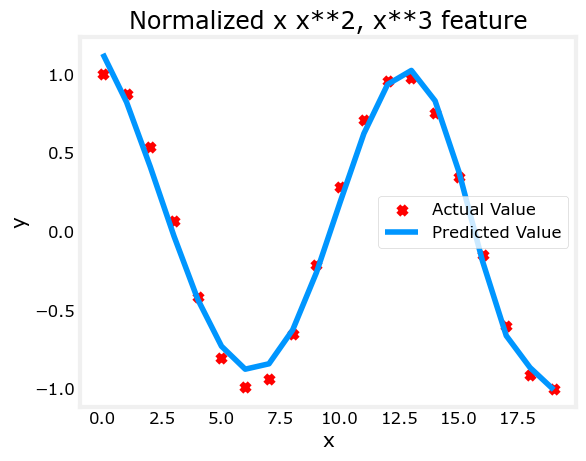
In this lab you: - learned how linear regression can model complex, even highly non-linear functions using feature engineering - recognized that it is important to apply feature scaling when doing feature engineering